Elisabetta Monari Martinez Department of Pure and Applied Mathematics, University of Padua, Padova, Italy¹ Katia Pellegrini Graduated student, Department of Psychology, University of Padua, Padova, Italy

Reprinted with the permission of the authors and Karin Beesley, Permissions Administrator, Taylor & Francis Group Preprint of an article whose final and definitive form has been published in European Journal of Special Needs Education © 2010 Copyright Taylor & Francis; available online at http://www.informaworld.com/0885-6257 To cite this article: Monari Martinez, E. and Pellegrini, K. (2010) Algebra and problem-solving in Down syndrome: a study with 15 teenagers, European Journal of Special Needs Education, 25(1), 13-29.

ABSTRACT. There is a common opinion that mathematics is difficult for persons with Down syndrome, because of a weakness in numeracy and in abstract thinking. Since 1996, some single case studies have suggested that new opportunities in mathematics are possible for these students: some of them learned algebra and also learned to use equations in problem solving. Here an educational study with 15 teenagers with Down syndrome is presented: fractions, percentages, first degree equations and problem solving with equations are taught and learning is monitored. The students' performances during the course and in a final test are compared: the students seem to have learned the new program and to remember it one month later. They seem to perform better with equations and problem solving with equations than with other more conventional topics. There are no significant differences in the performance of different gender groups.

Keywords: Down syndrome, mathematics, algebra, problem solving, mathematical education, special education.

Introduction

Are persons with Down syndrome hopeless at mathematics? Is it possible that their main difficulties are restricted to numeracy and in mental computation and do not involve the entire domain of mathematics? Little can be said about mathematical skills that require few computations, but more logic because almost nobody tries to teach these kinds of skills to students with Down syndrome. On the contrary, teachers insist on building up "the basics", which fall down as soon as the pupil gives an answer that makes no sense and then the teachers start all over again. Children with Down syndrome may sometimes produce nonsensical answers and this could happen more frequently when they are pushed to give an answer. Our hypothesis is that mathematics can be learned better in a parallel way by people with intellectual impairment, rather than in the traditional hierarchical way², because they seem to learn each part at a different rate: for instance, students with Down syndrome might be slower in numeracy than in elementary set theory, geometry and algebra. Therefore, a teenager, who is included in a mainstream class, might solve algebra exercises as well as his peers do - with the help of a calculator or of visual devices for the computation - while still working at an elementary level in numeracy tasks (Monari-Martinez, 2002). A common observation of parents is that children with Down syndrome are reasonable and logical in daily life, even if they sometimes appear to be immature: why should they be illogical in mathematics? At school, they have relatively good results in elementary set theory, which in the last century was considered by most mathematicians to be the basis of all mathematical culture (Aubin, 1997). A research study by Gherardini and Nocera (2000) asked Italian teachers from mainstream elementary schools (age: 6-11 yrs), middle schools (age: 11-14 yrs) and high schools (age: 14-19 yrs), what their 385 students with Down syndrome had achieved. On logic, the result was that around 70% of the students were able to build a set, defined by a property. Consistent with that work, an exploratory study by Danesi (2000) compared a group of 16 individuals with Down syndrome (aged between 7 and 25 years) to a mental age matched control group of typically developing children in logic-mathematic competences, and found no significant difference between the two groups. This result supports the hypothesis that their logic is not weak compared with their mental age. Therefore, since 1995, an aim of E. Monari-Martinez has been to study what topics students with Down syndrome are able to learn beyond numeracy, using compensatory tools such as calculators and visual supports for counting.

The first study was of two teenagers with Down syndrome who learned algebra in high school. They were included in mainstream classes, as in Italy the inclusion of students with any disability in mainstream secondary schools has been required by law since 1992, so it was natural to try to teach them the same subjects as their peers. The surprise was that they learned and enjoyed algebra, even if they continued to have difficulties with arithmetic (Monari-Martinez, 1998). Unfortunately, the biggest problem was not the difficulties of the students, who were happy and proud to learn, but the attitude of many teachers and experts who were sceptical about the program and therefore limited the students' right to learn. The most common question the teachers asked was "Is algebra useful to "these" students?" The answer might be "It is useful in the same way that it is for all other students". In fact, many adults, who have studied algebra in school, want their children to learn it too, because they believe in its "formative" value, which means it helps learning and reasoning in other subjects - even if they themselves never use algebra in their daily lives, and so remember only very little of the subject. Why should the same not be true for students with Down syndrome? This hostility towards an algebra program for students with Down syndrome reflects a more general opposition to teaching abstract topics, among which algebra is the first that all students have to face in a systematic way. In other words, the prejudice might be based on an assumption that they can never reach the Piagetian "formal operations stage" (Hunter, 2005; Piaget's theory, e.g. in cap.15 of Gazzaniga, Ivry, Mangun, 2002). As observed in (Monari-Martinez, 1998), algebra may be particularly useful for students with Down syndrome, because its formal language is unambiguous, concise and gives all the information needed at any stage. Moreover, the most frequent logical process used is to follow a sequence of instructions, which can also be written down at the beginning and kept handy - so can be used by students with Down syndrome even though they seem to have few difficulties in repeating remembered sequences in the right order (Kay-Raining Bird & Chapman, 1994). These and other experiences with algebra lead us to suppose that students with Down syndrome can handle abstract things in a relatively easy way, but that they have difficulty in working with too many things and too many relationships at the same time, because of their well-known weakness in working memory (Chapman & Hesketh, 2001; Jarrold & Baddeley, 2001). Consistent with that hypothesis, Gherardini and Nocera (2000) have established that these students are weaker in tests of mathematical problem solving (Jitendra, Griffin, Haria, Leh, Adams, Kaduvettoor, 2007; Reed, 1999), where they have to consider several objects and relationships together. In fact, in elementary and middle schools, around 70% of the students were not able to choose known operations to solve small problems (only around 5% were consistently successful), while around 25% were probably not taught on this topic, as their teachers did not reply to our requests for information. In secondary schools, this topic was rather less commonly studied; just 1% of students were reported to be able to solve these problems, while 56% appeared unable and in fully 43% of case, no data was available because teachers simply did not respond. In the four numerical operations, the same study shows better results than in problem solving, especially in addition and subtraction, if they were computed with the help of visual prompts such as real objects or drawings of the objects to count. Multiplication and division problems seem to be much more difficult, even using visual prompts: less than one-half of the students that succeeded in addition (mean 74%) and in subtraction (mean 64%) were able to do them (means, respectively, 28% and 22%). These results are consistent with others reported in literature on Down syndrome (Bird & Buckley, 2002; Buckley, Bird, Sacks, Archer, 2002; Carr, 2000). The four operations define the same order of increasing difficulty, from addition to division, for typical students; multiplication and division are much more difficult to learn than addition and subtraction (Dowker, 2005; pg. 42-44). Mental computation was difficult for the students, but they improved it by attending lessons, and they learned in the second decade of their life what is typically learned in the first, as has been observed for many other cognitive achievements (Nadel, 1995). Typical students were also found to have much better performance in written than in mental calculation (Thompson, 1997). However, these outcomes show that the improvement in operations does not seem to help with mathematical problem solving. In fact, the students' performances might be related not only to an impairment of working memory (Swanson, 2006; Swanson & Beebe-Frankenberger, 2004; Swanson, Cooney, & Brock, 1993), but also to difficulties in the classification of problems, i.e. to find the similarity between a particular problem with others that were solved before (Fuchs, Fuchs, Prentice, Burch, Hamlett, Owen et al. 2003; Fuchs, Fuchs, Prentice, Hamlett, Finelli, & Courey, 2004; Silver, 1979; Schoenfeld & Herrmann, 1982). Therefore, it might help to have fewer types of problems to consider. If students are taught to solve problems algebraically with equations, the number of types of problems to remember — or more specifically, the number of formulas to solve them — is reduced. For instance, if we have to solve the three following problems

In this way, we can divide the problem solving strategy into several steps: i) recognising the type of problem and finding the main relation among the variables; ii) understanding which variables are known and which are unknown; iii) substituting the values in the relation and writing the appropriate equation; iv) solving the equation; v) interpreting the solution of the equation in the context of the problem and verifying if it really solves the problem.

Usually, problem solving is not a linear process like that described here, but a dynamic process in which students have to go back and forth from one-step to another to correct their plan. The use of equations permits the transformation of a large part of that process into a mathematical procedure, which can be learned step by step.

The importance of algebra and, in particular, of linear equation solving, is recognized in mathematics education as a focal point for U.S. students in Grade 7 (12-13 year old) by the National Council of Teachers of Mathematics (Ballheim, 1999; National Council of Teachers of Mathematics, 2006; Rittle-Johnson & Star, 2007). Italian students typically approach the algebra curriculum and learn to use linear equations in problem solving in the last year of Middle school, in their 8^th year of school, when they are 13-14 years old - but this topic is completely refreshed during the next year in secondary schools. It seems that there are cross-cultural differences in approaches to algebra: the continental (Italy, France, Germany and Hungary) approach emphasizes symbolic manipulation and uses traditional word problems to introduce algebra, while the Anglophone (UK, Australia and Canada) approach is less formal and prefers to express algebraic problems in terms of more realistic 'problem situations' (Sutherland, 2002). The idea of introducing algebra to students with a lower-than-normal level of mathematical abilities is not new. In fact, considering the difficulties that students have in making the transition from arithmetic to algebra, some researchers, such as Davis (1985, 1989) and Vergnaud (1988), have proposed that the basic concepts of algebra should be introduced at an earlier age — perhaps grade 2 or 3 in primary school — consistent with the view espoused by the great French mathematician Dieudonne' (1960, Cf. Bodanskii, 1991), that arithmetic approaches to verbal problem-solving should be completely rejected in favour of algebraic methods when primary school begins. The proposal is further supported by Bodanskii (1991), whose experiments with Russian children produced outstanding results: fourth grade pupils solved verbal problems with equations better than their peers did with arithmetic methods, and this advantage was preserved even later, in the sixth and seventh grades, when their peers had also been introduced to algebraic methods with the traditional program (Schliemann, Carraher, Brizuela, Jones, 1998). Hence, "Early Algebra" projects blossomed. Some were more concerned with developing arithmetic reasoning in accordance with algebraic reasoning (e.g. Warren, 2003) than with the introduction of formal algebra in primary education. Others considered the appropriate use of algebraic notation throughout primary education, to support the development of mathematical concepts, and also introduced the concepts of function, number lines and graphs (Carraher, Schliemann, Brizuela & Earnest, 2006).

Previous studies on algebra in Down syndrome

The hypothesis of E. Monari Martinez was that as equations are used to simplify complex problems in very different fields, they could also be used to simplify problems that are not difficult for typically developing students, but very difficult for people with Down syndrome. The objection might be that equations are too difficult as tools, but the result of the first study on algebra learning of two teenagers with Down syndrome (1998) was more optimistic, suggesting that it might be worth trying to use them. That hypothesis was presented in 2001 as a challenge to the students of a course on Special Education for teachers from the University of Venice. Nives Benedetti, who had a student with Down syndrome in her class, agreed to try it in a single case study for her thesis. The result was impressive. Francesca, an 18 year old student with Down syndrome, who attended a mainstream secondary school for cooks, learned fractions, equations and the use of equations in problems. Moreover, she was able to apply them in the same exercises of Nutritional Science and of Business Administration as her schoolmates. This experience helped the girl mature and improved her self-esteem (Baccarin, Benedetti, Monari Martinez, 2004).

These promising results encouraged E. Monari Martinez to try to extend this experience to more students with Down syndrome, and this was realized with the collaboration of students in the University of Padua, during their dissertation projects. Another single case study was conducted by M.E. Baccarin, with a 14 year old boy with Down syndrome, who attended a mainstream middle school. This boy also enjoyed learning and improved his academic performance (Baccarin et al., 2004). A similar positive study was carried out by E. Michelini with 6 students with Down syndrome: she prepared a syllabus and monitored the students' learning in step by step fashion, as they were taught together in a course (Michelini, 2003). That study was followed by another by Neodo, with 6 students with Down syndrome, who learned fractions, equations, problem solving with equations and the first steps of analytical geometry (Neodo, 2004; Neodo & Monari Martinez, 2005).

The educational study

The study described in this paper was designed to verify if the experiences of previous single case studies, as cited above, could be extended to a larger number of students with Down syndrome. It was carried out by K. Pellegrini during her dissertation project (Pellegrini, 2003). Specific aims were: i) to verify if a mathematical syllabus, including simple algebraic equations and problem solving with equations, could be learned by a randomly chosen group students with Down syndrome during an individualized course; ii) to verify if they were able to retain what they had learnt - and any performance gain - for a month after the end of the course; iii) to study how each topic was learned and, in particular, how the algebraic topics were learned with respect to other more conventional topics, such as fractions and problem solving with objects; iv) to check if there were any differences in learning between genders; v) to compare these learning outcomes to those of a group of typically developing students, with the same nonverbal mental age, who were taught by another experimenter with a similar programme at school.

In this study, the dependent variable was the percent accuracy in the exercises, and we manipulated the kinds of exercises employed, the groups of participants that took them, and the testing times. We will report first, in detail, the study with the students with Down syndrome and later, briefly, the similar study of N. Corazza with typically developing students.

Participants

The main study was conducted with 15 adolescents with Down syndrome, 9 boys and 6 girls - chosen randomly living in the province of Milan, and with families that had also agreed to participate. Their age range was 13-15 years with a mean of 13.9 and a standard deviation (SD) of 0.68. All of them attended either middle or secondary mainstream schools in their neighbourhoods: this is common in Italy, because, since the '70s, attendance at mainstream (elementary and middle) schools has been compulsory for all children regardless of any disability that they might have. All the students who accepted an invitation to apply were included in the study with no constraints other than the age range (13-16) and the presence of Down syndrome. The study was carried out by the second author, as teacher and experimenter, in the students' homes - twice a week in the afternoon, for six months. The length of each session was from two to three hours, depending on the availability of the student and of the family, as well as on the difficulty of the topic that was taught and the acceptance of the student. Their nonverbal intelligence quotient (IQ) (range 66-73, mean 69, SD 2.20) and nonverbal mental age (MA) (range 9.1- 10, mean 9.6, SD 0.25) were estimated using an old version (1938) of the standardized test of Raven's Progressive Matrices (1954). We chose a test of nonverbal abilities because of the relative independence of many logical and mathematical abilities from verbal abilities (Butterworth, 1999), which are more impaired in Down syndrome in comparison with more general abilities (Chapman & Hesketh, 2001).

Materials and procedure

The exercises were prepared after looking at different textbooks of mathematics used in mainstream middle schools in Italy.

The topics from the curriculum that were taught in this study, were:

• Fractions and percentages: their visual representation, simplification, operations, and their use as operators;
• Algebraic equations, with rational coefficients, of the first degree, ax = b, or of the second degree, only as ax² = b;
• Problem solving with equations, using the relations:

  PART = FRACTION * WHOLE and
  PART = (PERCENTAGE ÷ 100) * WHOLE

• Problem solving with equation in physics, using the relations:

  s = v_A t          s = ½ g t²          v = g t

During each session, the experimenter presented the topic of the day, presenting some examples, and gave the students a notebook to write in with the exercises to be solved in the order that they were presented. All of the students received the same books and were allowed to use a pocket calculator, a table of prime numbers and a table of multiplications. They were allowed to draw or to use objects for counting. Every time a student was not able to reply to a question, the experimenter helped him/her by explaining the topic in greater detail, but recorded how much help he/she needed. Each question was therefore scored with 0 if the student did nothing by him/herself, with 1 if the student did something by him/herself, but not enough (less than 50%), with 2 if the student did a lot by him/herself (more than 50%), but not everything, with 3 if the student did everything by him/herself.

The score of each exercise was the average score of its questions. From these data, we were able to understand how each exercise was learned and to compare the students on each topic.

The exercises were the following:

1. The students were given 10 large rectangular cards, and asked to divide them into equal parts, colour some parts of their choice, and write the fraction corresponding to the coloured part as a proportion of the whole card.
2. Similar to exercise 1, but, instead of the cards, students were given drawings of different forms (circles, triangles, etc.,) that were already divided in equal parts to colour, before writing the corresponding fraction.
3. Students were given drawings of different forms, divided in equal parts and partially coloured, and were asked to write the fractions corresponding to the ratio between the coloured part and the whole.
4. Students were given uncoloured drawings of different forms, divided in equal parts, and a fraction for each of them, and asked to colour the part corresponding to the fraction.

5. Students were given tables with 10 equal rows and 10 equal columns; some coloured cells form different shapes and they were asked to write the percentage corresponding to the ratio of the coloured part to the whole table.
6. Students were given tables, already divided into 100 equal cells, as above, and a percentage number for each of them; they were asked to colour a part of the table corresponding to the given percentage.

7. Students were asked to decide if the association of a partially coloured drawing to a fraction was correct or not. The drawings were of different forms, but the division was sometimes into equal parts and sometimes into unequal ones.
8. Students were given partially coloured rectangles, drawn on a sheet that was already divided into small squares, and asked to write the fraction corresponding to the ratio between the coloured part and the whole. This exercise was different to exercise 3, because the rectangles were divided by the teacher into unequal parts and the students could not trust this division, which was confusing, but had to use the division into squares on the stamped sheet to calculate the ratio.

9. Multiplication of two written fractions, using the rule (a/b)*(c/d) = (a*c)/(b*d).
10. Multiplication of two simple fractions, using twice the fractions as operators on rectangles. Dividing the rectangles twice, they could look at a visualization of the previous rule.

11. Simplification of an expression as

    n

    n*m

12. Simplification of an expression as

    n*m

    n*p

13. Simplification of an expression as

    n

    n

14. Simplification of an expression as

    n	*	m
    m		n

15. Simplification of fractions, after decomposition into prime factors of the numerator and the denominator.
16. Simplification of fractions looking at a visualisation with rectangles.

17. Calculate

    a	of N (e.g.	3	of 200)
    b		8

18. Calculate

    a	*	c	of N
    b		d

19. Fraction as numerical operator for sets of objects (e.g. there are 15 flowers: 1/3 are violets, 1/3 are little roses and the others are daisies. How many violets, little roses and daisies are there?). The students had to solve the problems using a table, divided into numbered columns, and objects: in the example, they had to divide 15 stems (drawn on cards and cut out) into three equal parts and to put the different flowers (also on cards), onto the stems. The first three columns of the table were used to distribute the stems into equal parts and the students had to separate the different kinds of flowers, using the columns. They then had to count and write the answers.

20. What is equal? What is unequal? Looking at pairs of partially coloured rectangles, decide if they are equal or not.
21. Solve equations such as

    a	* N = x, where x is unknown (e.g.,	5	* 8 = x ), a, b and N are integers and N is a multiple of b
    b		4

22. Solve equations such as

    a	* x = N , where x will be an integer (N is a multiple of a).
    b

23. Solve equations such as x * a = N , where x will be a fraction.
24. Solve equations such as a% * N = x , where a, N are integers and x will be an integer (e.g., 9% * 70 = x)
25. Solve equations such as a% * x = N , where x will be an integer.
26. Solve equations such as x% * N = a , where x will be an integer.

27. Problems with the equation

    a	*N = x.
    b

28. Problems with the equation

    a	*x = N.
    b

29. Problems with the equation x * a = N.
30. Problems with the equation a% * N = x.
31. Problems with the equation a% * x = N.
32. Problems with the equation x% * N = a.
33. Problems of physics.

One month later, the experimenter asked each student to take a final test on the main topics studied, to check how much they were able to remember. These exercises were similar to the previous ones, but with fewer questions, as the test lasted not more than two sessions. The final test was presented and graded in the same way as the course, to mitigate any influence of the teacher's approach / attitude on the students' performance. Questions within each exercise were also very different, ensuring that corrections for previous questions could not help the students to answer future questions. The final test contained the following exercises:

1. Fractions I: From drawings to fractions, as in ex. 3 of the course;
2. Fractions II: From fractions to drawings, as in ex. 4 of the course;
3. Percents: From a coloured table to a percent number and the converse, as in exercises 5 and 6 of the course;
4. Contra-examples of fractions, as in ex. 7 of the course;
5. Simplification of fractions after the decomposition into prime factors, as in ex. 15;
6. Visual simplification of fractions, as in ex. 16;
7. Fractions as numerical operators, as in ex. 17;
8. Problems with objects: fractions as numerical operators on sets of objects, as in ex.19;
9. Equations with fractions, as in exercises 22 and 23;
10. Equations with percents, as in exercises 25 and 26;
11. Problems with equations, as in exercises 28, 31 and 32, and problems of physics, as in ex.33.

Some details on the scoring method

As mentioned above, each exercise will be considered, in order to understand what was more difficult, what was easier and what kinds of difficulties the students had. In the course, the experimenter proposed a different number of questions in each exercise, depending on the difficulties the students had: as the aim was to have them learn, we proposed more questions for difficult tasks, until almost everybody performed correctly. This gave us a scoring problem: the number of questions asked in the same exercise might change its final score because, if we continued asking questions, which most of the students were able to answer, we increased the mean score for that exercise. Therefore, we needed a general rule for averaging the scores for each exercise. To achieve that goal, we decided to consider and average, for each exercise, the first set of questions, from question 1 up to the first two that were answered without any help by all of the students, except for one student.

Results

With the above scoring rule, the number of questions in each exercise gives a measure of how much training was necessary in order for almost all the students to learn it, as shown in Figure 1.

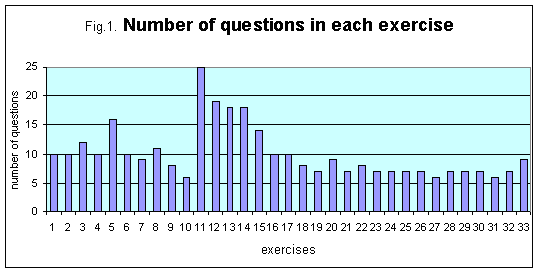Figure 1. The number of questions in each exercise gives a measure of how much training was necessary for almost all the students with Down syndrome to learn it.

As shown in Fig. 1, among exercises from 1 to 19 on fractions, exercise 5, the first that involved percentages, required more time to be learned by everybody, exercises 9 and 10, concerning the multiplication of fractions, were rather easier, and exercises 11 to 14, involving the simplification of numerical expressions, were particularly difficult, consistent with the previous studies mentioned above. The numerical expressions were respectively

In Fig. 2, for each exercise of the course, ordered according to the order of presentation, the mean accuracy among all the students is reported, as well as the lowest and the highest accuracy, and their respective trend lines (dotted lines indicating the linear regression lines). The accuracy (percent score) of each student in each exercise is obtained by averaging the percent scores in all its questions, that arise from raw scores (0-3).

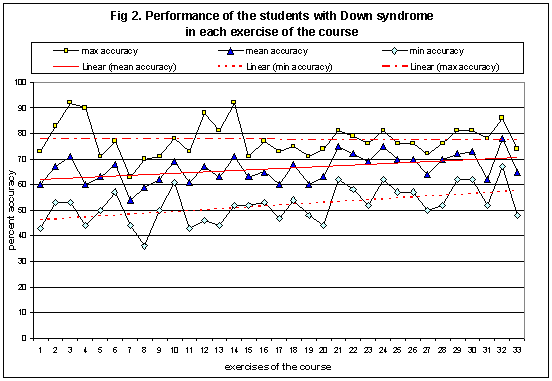Figure 2. Percent mean accuracy in each exercise of the course, with an indication of the maximum and the minimum accuracy obtained in each exercise. The trend lines are drawn for the mean, the minimum and the maximum accuracy in the exercises that are ordered by presentation time.

We can observe that the slope of the trend line (trend) of the mean accuracy is positive and significant (b_mean=0.273, t(31)=3.01, p=0.005), as is the trend of the minimum accuracy (b_min=0.356, t(31)=3.103, p=0.004), while the maximum accuracy trend is almost zero and not significant (b_max=-0.007, t(31)=-0.057, p=0.955). This means that in general there was an improvement of the lowest and the mean performances, and a preservation of the highest scores, throughout the course, even with new and abstract topics such as equations and problems with equations. Contra-examples of fractions (ex. 7 and 8) needed more help, as well as ex. 17 and 19 (which deal respectively with fractions as operators on numbers and on set of objects) and ex. 27, 31 and 33, which were new tasks. The problems with objects (ex. 19) were difficult at the beginning: even if it seems an elementary task, the use of objects confused some students who were not able to understand what they had to do. The positive results with equations and in most of the problems with equations suggest that the students had trouble with changes in the kind of tasks involved, e.g. from a written computation to a computation with objects, rather than with abstract concepts in themselves.

Figure 3 shows the comparison of the results during the course and in the final test: the mean percentage accuracy of all students in each exercise of the final test are compared with the mean percentage accuracy gained in all the similar exercises of the course for which we have calculated an average. One month after the end of the course, it can be seen that there was a general improvement in performance, on average, in the final test in comparison with the course - as well as either an improvement or a preservation of performance on average, in each exercise. The exercises are ordered according to the temporal order in which they were presented both in the course and in the final test.

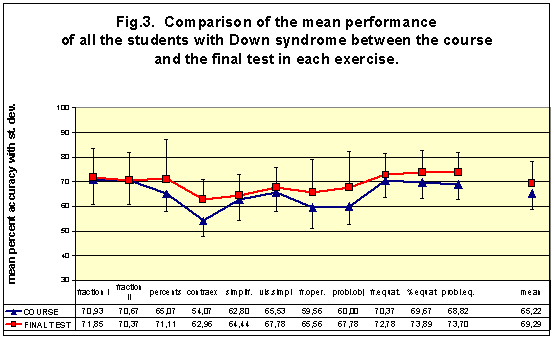Figure 3. The mean percent accuracy in the exercises of the final test and the corresponding exercises of the course are compared. The bars indicate the standard deviation for each exercise.

Using a within-subjects design, we explored the differences in the students' performances both between the exercises and between the course and the final test. A repeated measures analysis of variance (ANOVA) revealed some significant differences in performance as the exercises proceeded. In fact, the students were significantly poorer in the contra-examples of fractions than they were in both the previous exercise on percentages (F(1,14)=23.834, p<0.001) and the subsequent exercise on the simplification of fractions (F(1,14)=15.909, p=0.001). The students performed significantly better on the visual simplification of fractions than they did with the previous exercise on numerical simplification (F(1,14)=6.878, p=0.020) and with the subsequent exercise on the use of fractions as numerical operators (F(1,14)=6.694, p=0.022); this confirms the well known strength of people with Down syndrome in visual tasks. It is surprising that, with equations, a new and abstract topic, the students performed significantly better than with problems with objects (F(1,14)=26.256, p«0.001), which is a more concrete task that is often preferred by teachers for students with Down syndrome. In the final test, the mean improvement with respect to the course was significant (F(1,14)=10.823, p=0.005), but, in general, there was no relative change in performance, i.e. the easier and more difficult exercises in the course remained easier and more difficult in the final test. The exception was in the passage from the exercise on contra-examples of fractions to the simplification of fractions, where the improvement in the final test was much stronger in the former than in the latter (F(1,14)=7.507, p=0.016).

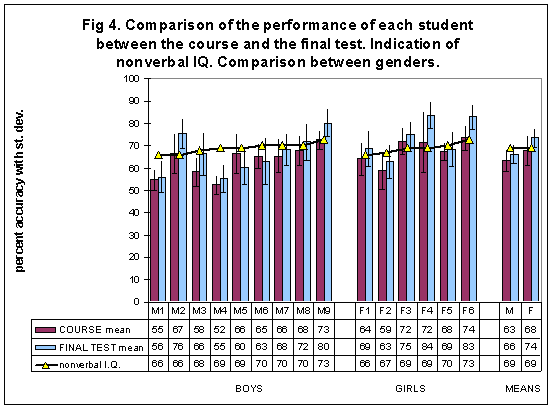Figure 4. Comparison of the mean accuracy (with SD bars) of each student with Down syndrome, in the course and in the final test. Comparison between genders. Indication of the nonverbal IQ of each student, measured with the Raven's matrices.

If we look at the performances of each student in the final test in comparison with their performances in similar exercises during the course (Fig. 4), we observe that only one boy (M5) got significantly worse (at the paired t-test, t(10)= -2.525, p=0.03), two boys and two girls significantly improved (respectively, M2 with t(10)=3.382 and p=0.007, M9 with t(10)=5.595 and p<0.001, F4 with t(10)=3.576 and p=0.005, F6 with t(10)=6.557 and p<0.001) and all of the others displayed preserved performances. The mean improvement in performance from the course to the final test was significant for both the male group (repeated measures ANOVA, with the exercises as the first independent variable, F(1,10)=13.536 and p=0.004) and the female group (F(1,10)=14.847 and p=0.003). The students, then, seemed to have learned the program and to remember it after one month. There was a significant correlation between the students' nonverbal I.Q. score and their mean accuracy in the course (Pearson, r(13)=0.593, p=0.020), but not in the final test (Pearson, r(13)=0.483, p=0.068).

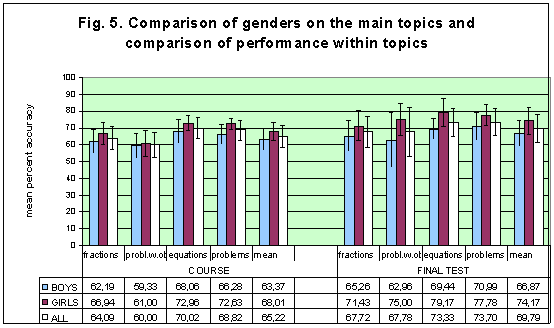Figure 5. Comparison within topics of the mean accuracy (with SD bars) gained by the students with Down syndrome in the course and in the final test, and comparison between genders.

In Fig. 5 we compared the genders in performance during the course and in the final test, with regard to some main topics, such as fractions, problems with objects, equations and problems with equations, where the accuracy on each topic is the average of the accuracy on similar exercises. The difference between the genders in general is not significant in the repeated measures ANOVA, with the students as first independent variable, (F(1,13)=3.547 and p=0.082). Comparing the performances of all students within the topics, the students performed significantly better with equations than both fractions (pair wise comparison with Bonferroni's adjustment: p<0.001) and problems with objects (p=0.001). They performed significantly better in problems with equations than both in problems with objects (p=0.004) and in fractions (p<0.001), while the other differences were not significant. In fact the test of within-subject contrasts reveals that there was no significant difference in performance between fractions and problems with objects (F(1,13)=3.283, p=0.093) or between equations and problems with equations (F(1,13)=0.741, p=0.405), but the improvement was significant between problems with objects and equations (F(1,13)=26.025, p<0.001). The experimenter observed that equations and problem solving with equations were the favourite topics. Comparing the performance of all students between the course and the final test on the main topics, we observe that there was a significant mean improvement (repeated measure ANOVA, F(1,14)=16.551, p=0.001). Comparing the course and the final test, significant mean improvements occur on fractions, on problems with objects and on problems with equations (with paired t-tests: t(14)=2.672 and p=0.018, t(14)=2.481 and p=0.026, and t(14)=4.058 and p=0.001 respectively), while the improvement on equations was not significant (t(14)=2.005 and p=0.065).

Discussion

The results of this study are similar to the previous results obtained by Monari-Martinez and colleagues in single case studies: the students displayed the same strengths and the same difficulties. In this research, as in most of the previous cases, the experimenter was both instructor and tester: from an experimental point of view, this occurrence might be a weakness in terms of internal validity, as the expectations of the experimenter might have influenced the outcomes, but, conversely, from an educative point of view, this is the usual procedure in all schools. In fact, it is well known that new testers can negatively influence the performance of typical developing students. Why should students with Down syndrome need a stricter procedure than typically developing students? Another argument in favour of this approach is that, in this case, the tests are presented more with the aim of teaching than with the aim of testing: indeed, we measure how much help the students needed to succeed, so can monitor their learning at every intermediate step. This information is essential to experimenters who deal with people with atypical development, such as Down syndrome students, on new topics. To overcome this methodological problem, a more expensive solution might be to have two experimenters working together at all times, in different functions (instructor and tester), so that both might be able to be familiar with the students. Another solution may be to have more trials, carried out by different researchers or to teach these topics to students with Down syndrome in the mainstream schools, so that everyone can check the reliability of the results. This approach has been tried successfully with four teenagers who learned algebra at school (Baccarin, Benedetti, Monari Martinez, 2004; Monari Martinez, 1998): working in the same classroom at the same time as their typically developing schoolmates, these students were able to do almost the same tests without any extra support.

Looking at the results of this study, we have seen that the problems with objects were difficult at the beginning, even if there was an improvement later, while equations, which imply a logic task, were easier right from the start. This contrasts with the usual belief that children with Down syndrome deal better with objects than with abstract concepts. During the course, we observed that the students had difficulties with sudden changes in task-types, rather than with abstract subjects in themselves. For instance, they required a longer time to learn the simplification of fractions such as 5/5, which usually seems very simple, than the simplification of 4/6, which looks more difficult, perhaps because in the first case they had to apply a rule instead of applying the usual procedure for simplification, as in the second example. This problem with task-changes might be considered a difficulty in inhibiting a current active schema to shift to a new one. This trouble can be considered a consequence of a more general deficit in executive functions, as observed in (Chapman & Hesketh, 2001). On the other hand, the success in algebra might be ascribed to the visualization of abstract concepts in written formulas that are also managed visually (Landy & Goldstone) and visual tasks are well-known strength of students with Down syndrome (Chapman & Hesketh, 2001).

The students with Down syndrome also retained, one month after the end of the course, what they had learned: there was an improvement in their performance, on average, in the final test in comparison with the course, as well as either an improvement or a preservation of the performances in each exercise.

We observed that except for one boy, who got significantly worse, all of the students either significantly improved (two boys and two girls) or preserved their performance in the final test in comparison with the course and there was a significant correlation between their nonverbal I.Q. and their mean performance score in the course.

Considering gender, there was no significant difference between males and females, on average, in the course and in the final test, but the two groups were also too small to capture statistically significant differences, unless those differences were very extreme indeed. Comparing the topics, we observed that equations and problem solving with equations were the students' most successful subjects, but there was also a significant improvement, in the final test, in fractions and problems with objects.

To study how typically developing students with similar nonverbal mental age could face this program, Nadia Corazza taught a similar curriculum in an elementary school class of 19 typically developing students in the 4^th grade, aged 9 to 10 years (Corazza, 2003). The results were similar to those with students with Down syndrome, even if the different learning environment of the two groups — individually at home for the Down syndrome group and all together at school for the typically developing group — discourage from a direct comparison. Anyway the students' age seemed to play some role: when she tried to teach the same programme to younger typically developing students in a 2nd grade class (7-8 yrs), she was unsuccessful and had to reduce the programme, dropping the equations and the problems with equations (Corazza, 2003).

In conclusion, even if other studies may be necessary to confirm these results, this experience suggests that students with Down syndrome can progress, in the mathematical curriculum, and reach some secondary school level topics (regardless their abstractness), if the usual facilities are provided, both in text adaptation and in computation. Of course, the inclusion of these students in mainstream schools plays an important role in getting both the students and their families involved in this kind of programme.

Footnotes

1. Requests for information should be addressed to:
   Elisabetta Monari Martinez, Dipartimento di Matematica Pura ed Applicata, Torre Archimede, via Trieste, 63, 35121 Padova, Italy.
   Tel. 0039 049 8271446, Fax 0039 049 827 1499
   (E-mail: martinez@math.unipd.it)
2. Underhill (1983) also rejected the view of a unique learning hierarchy in the mathematics education of typical students, and, A. Dowker (2005, pg 93-95) observed that some students with learning difficulties were not able to count, even though they did display other abilities like problem solving.

Acknowledgements

References

Aubin, D. (1997) The Withering Immortality of Nicolas Bourbaki: A Cultural Connector at the Confluence of Mathematics, Structuralism, and the Oulipo in France. Science in Context, 10 (2), 297-342.

Baccarin M.E., Benedetti N., Monari Martinez E. (2004) Strategie per avviare studenti con disabilità alla matematica "avanzata": equazioni e geometria analitica. (Strategies to initiate students with intellectual disability to "advanced" mathematics: equations and analytic geometry). Difficoltà di apprendimento 10 (2), 183-200.

Ballheim, C. (1999, October). Readers respond to what's basic. Mathematics Education Dialogues, 3, 11.

Bird G. & Buckley S. (2002) Number skills development for teenagers with Down syndrome (11-16 years). Portsmouth, UK: The Down Syndrome Educational Trust.

Bodanskii, F. (1991). The formation of an algebraic method of problem solving in primary school children. In V. Davidov (Ed.), Soviet studies in mathematics education. Psychological abilities of primary school children in learning mathematics (vol. 6, pp. 275-338). Reston, VA: NCTM.

Buckley, S., Bird, G., Sacks, B., Archer, T. (2002). A comparison of mainstream and special school education for teenagers with Down syndrome: Effects on social and academic development. Down Syndrome News and Update, 2, 46-54.

Butterworth, B. (1999). The mathematical brain. London: MacMillan.

Carr, J. (2000). Intellectual and daily living skills of 30-year-olds with Down's Syndrome: continuation of a longitudinal study. Journal of Applied Research in Intellectual Disabilities. 13, 1-16.

Carraher, D., Schliemann, A.D., Brizuela, B., & Earnest, D. (2006). Arithmetic and Algebra in early Mathematics Education. Journal for Research in Mathematics Education, Vol 37 (2), 87-115.

Chapman R. S, and Hesketh L. J. (2001). Language, cognition, and short-term memory in individuals with Down syndrome. Down Syndrome Research and Practice, 7(1), 1-7.

Corazza N. (2003) L'uso di equazioni per la soluzione di problemi nella scuola elementare: una studio nelle classi 2° e 4°. (Teaching problem solving with equations in an elementary school: a study with 2° and 4° grade students) Unpublished thesis, Padua: University of Padua.

Danesi, S. (2000) Le competenze logico-matematiche nella sindrome di Down: uno studio esplorativo. (Logic-mathematic competences in Down syndrome: an explorative study). Unpublished thesis, Padua: University of Padua.

Davis, R. (1985). ICME-5 Report: Algebraic thinking in the early grades. Journal of Mathematical Behavior, 4, 195-208.

Davis, R. (1989). Theoretical considerations: Research studies in how humans think about algebra. In S. Wagner & C. Kieran (Eds.) Research Issues in the Learning and Teaching of Algebra (vol. 4, pp. 266-274). Reston, VA: NCTM/Erlbaum.

Dowker, A. (2005). Individual Differences in Arithmetic: Implications for psychology, neuroscience and education. Hove, UK: Psychology Press.

Fuchs, L. S., Fuchs, D., Prentice, K., Burch, M., Hamlett, C. L., Owen, R., et al. (2003). Explicitly teaching for transfer: Effects on third-grade students' mathematical problem solving. Journal of Educational Psychology, 95, 293-305.

Fuchs, L. S., Fuchs, D., Prentice, K., Hamlett, C. L., Finelli, R., & Courey, S. J. (2004). Enhancing mathematical problem solving among third grade students with schema-based instruction. Journal of Educational Psychology, 96, 635-647.

Gazzaniga, M.S., Ivry, R.B., Mangun, G.R. (2002). Cognitive Neuroscience: the biology of the mind. 2^nd Edition. New York: W. W. Norton & Company, Inc.

Gherardini, P. & Nocera, S. (2000) L'integrazione scolastica delle persone Down: una ricerca sugli indicatori di qualità in Italia. (The inclusion in mainstream schools of persons with Down syndrome: a study on quality indicators in Italy). Centro Studi Erichson, Trento (Italy).

Hunter, A.G.W. (2005). Down Syndrome. In S.B. Cassidy & J.E. Allanson (Eds) Management of Genetic Syndromes, 2^nd Edition. Hoboken (NJ): John Wiley & Sons, Inc., pp. 191-210.

Jitendra, A. K., Griffin, C.C., Haria, P., Leh J., Adams, A., Kaduvettoor, A. (2007). A Comparison of Single and Multiple Strategy Instruction on Third-Grade Students' Mathematical Problem Solving. Journal of Educational Psychology, 99 (1), 115-127.

Jarrold C., and Baddeley A. D. (2001). Short-term memory in Down syndrome: Applying the working memory model. Down Syndrome Research and Practice, 7(1), 17-23.

Kay-Raining Bird, E. & Chapman, R. (1994) Sequential Recall in Individuals with Down Syndrome. Journal of Speech and Hearing Research, 37, 1369-1380.

Landy D. & Goldstone R.L. (2007). How Abstract Is Symbolic Thought? Journal of Experimental Psychology: Learning, Memory, and Cognition, 33 (4) 720-733.

Michelini E. (2003) L'apprendimento matematico in adolescenti con sindrome di Down: un percorso di matematica avanzata (Mathematical learning in teenagers with Down syndrome: a course of advanced mathematics). Unpublished thesis, Padua: University of Padua.

Monari Martinez E. (1998) Teenagers with Down Syndrome Study Algebra in High School. Down Syndrome: Research and Practice 5 (1), 34-38.

Monari Martinez E. (2002) Learning mathematics at school ... and later on. Down Syndrome News and Update 2 (1), 19-23.

Nadel L. (1995) Neural and Cognitive Development in Down Syndrome. In Nadel L. & Rosenthal D. (eds) Down Syndrome: Living and Learning in the Community, Wiley-Liss, New York, pp 107-114.

National Council of Teachers of Mathematics. (2006). Curriculum focal points for prekindergarten through grade 8 mathematics. Reston, VA: Author.

Neodo K. (2004) Elementi di geometria analitica:uno studio sperimentale con adolescenti con la sindrome di Down. (Elements of Analytic Geometry: an experimental study with adolescents with Down syndrome) Unpublished thesis, Padua: University of Padua.

Neodo K. & Monari Martinez E. (2005) Insegnare geometria analitica ad adolescenti con sindrome di Down: uno studio esplorativo. (Teaching Analytic Geometry to adolescents with Down syndrome: an explorative study.) In Davoli A., Imperiale R., Piochi B., Sandri P. (eds) Alunni, insegnanti, matematica: Progettare, animare, integrare.(Students, teachers, mathematics: planning, involving, including) Pitagora Editrice, Bologna, pp. 227-230.

Pellegrini K. (2003) Sindrome di Down e soluzione di problemi tramite equazioni: uno studio esplorativo.(Down syndrome and problem solving with equations: an explorative study) Unpublished thesis, Padua: University of Padua.

Raven J.C. (1954) Progressive Matrices 1938: Serie A, B, C, D, E. Edizione Italiana. Organizzazioni Speciali, Firenze (Italy).

Reed, S.K. (1999) Word Problems: Research and Curriculum Reform. Lawrence Erlbaum Associetes, Mahwah, NJ (USA).

Rittle-Johnson, B. & Star, J.R. (2007). Does Comparing Solution Methods Facilitate Conceptual and Procedural Knowledge? An Experimental Study on Learning to Solve Equations. Journal of Educational Psychology, 99 (3), 561-574.

Schliemann, A.D., Carraher, D.W., Brizuela, B., & Jones W. (1998). Solving algebra problems before algebra instruction. Paper presented at the Second Meeting of the Early Algebra Research Group. Tufts University, Medford, MA, USA.

Schoenfeld, A.H. & Herrmann, D. (1982). Problem perception and knowledge structure in expert and novice mathematical problem solvers. Journal of Experimental Psychology: Learning, Memory and Cognition, 8, 484-494.

Silver, E.A. (1979). Student perceptions of relatedness among mathematical verbal problems. Journal of Research in Mathematics Education, 10 (3), 195-210.

Sutherland R. (2002). A comparative study of algebra curricula. London: QCA.

Swanson, H.L. (2006). Cross-sectional and incremental changes in working memory and mathematical problem solving. Journal of Educational Psychology, 98 (2), 265.

Swanson, H.L. & Beebe-Frankenberger, M. (2004). The relationship between working memory and mathematical problem solving in children at risk and not at risk for serious math difficulties. Journal of Educational Psychology, 96 (3), 471-491.

Swanson, H.L., Cooney, J.B., Brock, S. (1993) The influence of working memory and classification ability of children's word problem solution. Journal of Experimental Child Psychology, 55, 374-395.

Thompson, I. (1997). Mental and written algorithms: Can the gap be breached? In I. Thompson (Ed.) Teaching and learning early number. Buckingham: Open University Press.

Underhill, R. (1983). Diagnosing mathematics difficulties. Columbus, OH: Merrill.

Vergnaud, G. (1988). Long terme et court terme dans l'apprentissage de l'algèbre. In C.Laborde (Ed.) Actes du premier colloque franco-allemand de didactique des mathématiques et de l'informatique (pp. 189-199). Paris: La Pensé Sauvage.

Warren. E. (2003). The role of arithmetic structure in the transition from arithmetic to algebra. Mathematics Education Research Journal, 15(2), 122.