Pnina S. Klein, Ed.D., and Mary Arieli, M.A.
Bar-Ilan University
Baker Center for the Study of Developmental Disorders in Infants and Children
Ramat-Gan 52900 Israel
|
Journal of Developmental and Learning Disorders 2(1): 299-319 (1997) Pnina S. Klein, Ed.D., and Mary Arieli, M.A. Bar-Ilan University Baker Center for the Study of Developmental Disorders in Infants and Children Ramat-Gan 52900 Israel |
Reprinted with the permission of Susan Wilson |
Abstract. Commonly used methods for developing math readiness in young children frequently do not meet the needs of children with various developmental disorders. Furthermore, children may learn to use skills (such as counting by rote memory) that may be misused and actually interfere with the future development of their mathematical thinking. This study presents a model for designing a remedial approach for a population of children with special needs, including children with severe problems involving the understanding and use of numbers. The Mediational Intervention in Math (MIM) shifts the focus of training from the auditory sequential mode to the visual simultaneous mode ("right hemisphere"). In addition, the MIM approach exemplifies the use of a mediational approach in math. Subjects were thirty children with Down Syndrome, 5 to 7 years old. The subjects were randomly divided into two groups. Group 1 received weekly training using the MIM approach, Group 2 did not participate in the program but their parents participated in MIM counseling including general information about the development of math skills and the MIM. Group 3 included children who were involved in an ongoing language and math enrichment program for one to three years. The MIM training lasted about 6 months. Six months following the intervention, a significant difference in children's performance on the Key Math Diagnostic Arithmetic Test was found in favor of Group 1. The children in Group 1 demonstrated a better understanding of basic mathematical concepts and problem solving abilities than the children in both other groups.
A developmental perspective has been gradually applied to a wider array of clinical populations including children with Down Syndrome (DS) (Hodapp & Zigler, 1990). Many children with developmental delays display an uneven profile of cognitive processing. Consequently, the commonly used practices of teaching literacy or math readiness skills may not yield the desired educational outcomes when used with populations of children with special needs. In math, for example, readiness skills most commonly include counting. Children with DS as well as children with Attention Deficit Disorder (ADD) and Pervasive Deficit Disorder (PDD) frequently learn to count by rote memory but are unable to apply this skill in situations requiring mathematical thinking and problem solving. Furthermore, most of the remedial math materials include concrete objects requiring sequences of motor activities, and the latter may present a real problem to children who have motor planning difficulties. The current study presents the special needs of one group of children, children with DS, and an attempt to design and implement a math program that is specifically suitable for their special needs.
Down Syndrome occurs in approximately 1 out of every 600 live births (Hook, 1982). DS may be caused by several types of chromosomal abnormalities resulting in the presence of three doses of chromosome 21 (e.g., trisomy of the 21st chromosome in all body cells, in part of them [mosaicism], or translocation of chromosome 21 or part of it to another chromosome [Cicchetti & Beeghly, 1990]). Individuals with DS display a wide range of intellectual levels from profound to mild retardation, with some reported cases of individuals of average intelligence (Fishier, 1975; Klein, 1996). Children with DS seem to progress in the same developmental sequence as that followed by nonretarded children (Weisz & Zigler, 1979). Kopp (1983) reviewed studies comparing the early development of children with DS and premature children with the development of nonretarded children. Infants with DS were found to develop along similar sequences in sensorimotor functioning (Cicchetti & Mans-Wagener 1987); in social smiling and laughter (Cicchetti & Sroufe, 1976); in play (Hill & McClure-Nicholich, 1981); and in language development (Fowler, 1990) as nonretarded children.
Children with DS have been reported to achieve considerable levels of competence in many areas of functioning, including social and cognitive situations requiring complex problem-solving skills. It is no longer surprising to find young DS children who read and write (Buckley, 1985; Irwin, 1989) or who can be integrated into regular classrooms quite successfully. It is, however, still repeatedly reported that despite the developments in other areas (Gibson, 1978; Buckley 1985), mathematical abilities of DS children are very poor as com pared to their functioning in other areas.
In view of the above it is rather surprising that very little attention has been directed toward research of this problem. Consequently there were only limited attempts to design early intervention programs that could help DS children overcome the problem of dealing with numbers and adjusting to the everyday demands of understanding the use of numbers (money, sizes, calendar, temperature, weights. etc.). The scarcity of research in this area could best be demonstrated by the fact that in the past 25 years only eight studies were reported on the subject and found in the ERIC and APA database,
Down Syndrome children have great difficulties in understanding and using mathematics. Difficulties in the formation and understanding of number concepts and calculations are called dyscalculia. It has been estimated that about 6 percent of the normal population has dyscalculia stemming from dysfunction of those areas of the brain involved in mathematical processing (Sharma & Loveless, 1986).
Numerous early intervention programs in mathematics have been introduced for children with special needs in this area of functioning in the past two decades (Bereker & Englemann, 1966; Horowitz, 1987; Mosley, 1986; Murphy, Bates, & Anderson, 1984; Stern, 1987). These programs were designed primarily for children with an IQ within the normal range and did not serve the special needs of children with DS. Only a few research studies on mathematical abilities of children with DS have been reported. Yarmish (1988) studied the development of conservation of number and substance in children with DS. He concluded that the introduction of variables such as color, size, and form decrease the problem-solving efficacy of DS children. Children with DS found it easier to discriminate between groups containing different numbers of elements when the differences between these groups was visually markable.
Several findings highlight characteristic behaviors of DS children attempting to handle mathematical tasks. The following is a summary of these findings:
Yarmish (1988) concludes that DS children could benefit from a method that will enable them to identify quantities visually and globally with no need to count. In addition, he claims that DS children lack strategies for coping with mathematical problems and could benefit from learning some of those strategies. Kelly and Schoen (1988) recommend a reward system that combines a verbal and a token reward as effective in reducing unwanted behavior and shortening response time in math problem-solving situations.
Is the development of mathematical reasoning of DS children different from that of normal children or is it merely slower? Lister, Leach, and Riley (1989) found that the developmental sequence leading to the formation of number concepts in DS children is similar to that found for normal children but it occurs later in time.
The intervention program described in the current study is based on the research discussed earlier and on the mediational approach to early intervention presented in a previous issue of this Journal (Klein, 1997) was modified for young DS children. This program has seen used successfully with individual children and has been modified and improved through this process prior to its use in the present study.
The MIM program is based on the general principles of Mediated Learning Experience (Feuerstein, 1979) and on the MISC (Mediational Intervention for Sensitizing Caregivers) program (Klein, 1990, 1992b, 1996; Klein & Alony, 1993), which is designed to sensitize adults to the special needs of young children, to their own objectives in mediating to them, and to the possible potential effects of their mediation (teaching behaviors) on the children's readiness to learn from new experiences. In addition, the program focuses directly on the enhancement of mathematical abilities in DS children.
The MIM includes two components:
Consequently, counting is taught first because it is considered a basic skill that must be learned, and upon which other stages of instruction are based. Children with DS have been found to learn how to count correctly but they were unable to use this skill in order to carry out any mathematical calculations. By the time they finished counting they either forgot the problem or were unable to use the counting to solve it. The MIM was designed to overcome this difficulty by shifting the focus of math problem solving from the left hemisphere sequential processing to the right hemisphere visual, global pictorial processing.
In order to enhance automatization of quantity identification without the need for counting, the program starts with the number 5 in the following configuration (:·:). Once this configuration is automatically identified across many variations of objects, other quantities are presented in a similar manner as derivatives of the original number 5. Rather than starting with the number one, as is traditionally done, we start with 5 since it has been found to be more efficient to progress from 5 in both upward and downward directions; namely, to learn quantities that are smaller and larger than 5. Five is easily identified by the children and is readily available for verification in the form of their own five fingers. The automatization of the 5 makes it easier to proceed to the construction of 10, which is a basic unit.
The MIM is designed to help children with a variety of difficulties in math. In fact, it focuses on different types of identified dyscalculia: verbal dyscalculia, apraxic dyscalculia, graphic dyscalculia, ideagnostic and operational dyscalculia.
Although the MISC has been applied cross-culturally with high risk infants and young children (Klein, 1996, 1997), the MIM program has been used with individual children with DS and other developmental disabilities, the current study is the first to examine the effects of the MIM on mathematical abilities of children with Down Syndrome.
There is considerable variability in the development of DS children. Based on research conducted in the past 20 years, DS children who have participated in early educational intervention programs, frequently function on a level enabling them to be included in regular education programs and to live normal lives within their family and community (Feuerstein, Rand, & Rynders, 1988). However, almost all DS children have great difficulties in understanding and using mathematics.
The MIM is part of the MISC-DS, one of a series of MISC programs implemented with infants and young children with special needs. The MISC is based on the theory of Mediated Learning Experience (MLE) that has been in use in special education for over 30 years, its clinical value having already been demonstrated (i.e., Feuerstein, 1979; Feuerstein et al., 1988). Originally designed for adolescent populations, MLE has more recently been tested in studies of early childhood and infancy (Klein, 1996, 1997; Klein & Alony, 1993; Klein & Feuerstein, 1984; Klein, Wieder, & Greenspan, 1987). The basic hypothesis in these studies was that primary factors affecting variations in the modifiability of children's cognitive functioning is the kind and amount of MLE they experience. Thus an attempt to increase a child's capacity to benefit from new experiences must focus on improving the kind of MLE he or she is exposed to. Mediated learning, as distinct from direct learning through the senses, occurs when the environment is interpreted for the child by another person who understands the child's needs, interests, and capacities, and takes an active role in making components of that environment as well as of the past and future experiences compatible with the child's needs and abilities. Mediation affects the individual's present learning and improves his or her opportunity to learn from future experiences.
Basically, MLE serves to maximize learning from experience. It is universal, not specific to one culture or type of content. It enables further change of the individual through direct exposure to stimuli, and allows a child to acquire basic structures that prepare him or her for future development (for more information on the mediational approach, Klein [1997]).
Five kinds of adult-child interactions that constitute MLE were defined in this study as follows:
Intentionality and reciprocity includes any act or a sequence of acts on the part of an adult that appears to be directed toward achieving a change in the child's perception, processing, or response (i.e., selecting, exaggerating, accentuating, scheduling, grouping sequencing, or pacing stimuli). A behavior that is intentional is considered reciprocal when the infant or child in the interaction responds vocally, verbally, or nonverbally, even by visual focusing, to an adult's behavior. Talking or handing a toy to a child, for example, is counted as showing intentionality and reciprocity only when it is clear that the parent's behavior is not accidental, and when there is an observable response from the child that she or he saw or heard the intentional behavior. An example of intentional behavior would include a parent making a visible effort to change his or her behavior and the environment, bringing an object to the child, moving it back and forth, observing the child and continuing to adjust the stimulus until the child focuses on it. Or the parent might move a bottle or a particular food item in front of the infant's eyes until he or she focuses on it. Such an action as placing toys into the bathwater would be intentional, as would facing the child and obtaining eye to eye contact, or placing an object in front of the child but at some distance, so he or she could attempt to reach it.
An adult's behavior that expresses verbal or nonverbal appreciation or affect in relation to objects, animals, or concepts and values. These behaviors may include facial gestures (e.g., exaggerated opening of the eyes and mouth), sounds, classification or labeling, and valuing the child's or adult's experiences (e.g., "Look, I am washing your foot now"; "See how long this macaroni is"; "Look at this beautiful flower"; "This cup is special, it belonged to grandfather").
An adult's behavior directed toward the expansion of a child's cognitive awareness, beyond what is necessary to satisfy the immediate need that triggered the interaction, may be considered as transcendence (e.g., talking to a child about the food during feeding is beyond what is necessary to assure provision of nutrition; exploring body parts or characteristics of water during bathing is not necessary for cleansing the body). Transcendence can be expressed through inductive and deductive reasoning, spontaneous comparisons, clarifying spatial and temporal orientation, pointing out strategies for short-and long-term memory, and for memory search and recall.
Mediated feelings of competence include any verbal or nonverbal behavior by an adult that expresses satisfaction with a child's behavior and identifies a specific component or components of the child's behavior that the adult considers successful. This process of identification can be carried out, for example, through timing of the verbal or gestural expression of satisfaction, through repetition of the desired behavior, or through its verbal identification (e.g., saying "good," "wonderful," "great," "yes," or clapping hands and smiling when the child completes a task or part of it successfully).
Mediated regulation of behavior includes adult behaviors that model, demonstrate, and/or verbally suggest to the child regulation of behavior in relation to the nature of the task, or to any other behavior. These may be expressed, for example, through processes of matching the task requirements with the child's capacity and interests, as well as through organizing and sequencing steps toward success. For example, "It is hot, cool it first before putting it in your mouth"; "Let's wash your face, slowly, so no soap will get into your eyes"; "Slowly, not so hard, it is delicate, do it softly", "First, turn all the pieces over, then search for the right piece." Mediated regulation of behavior may be related to processes of perception (e.g., systematic exploration); to the process of elaboration (i.e., planning behavior); or to processes of expressive behavior (i.e., reducing egocentric expressions and regulating intensity and speed of behavior).
The criteria of MLE were empirically defined (Klein & Alony, 1993; Klein & Feuerstein, 1984; Klein, Raziel, Brish, & Birenbaum, 1987) and developed into an observation scale yielding a profile of mediation that is based on the frequency of appearance of the behaviors exemplifying each of the criteria.
Using the frequency of appearance of MLE criteria, it was possible to predict the quality of parent-child interaction and of the child's cognitive performance at least four years following the initial observations (Klein, Weider, & Greenspan, 1987). It was also found that the criteria of a quality observation predicted infant development more accurately than measures of socioeconomic status (SES), of early physical condition, birthweight, Apgar, or even early measures of infant's intelligence (Klein, Raziel et al., 1987).
These criteria of mediation relate to focusing behavior, exciting and associating experiences with meaning, expanding and elaborating behaviors, goal-setting behaviors, processes involving regulation of behavior, and mediation of competence.
The frequency of appearance of behaviors that represent the above criteria of mediation determine the quality of a teaching interaction between a child and another person. It is reasonable to assume that high quality mediation may consequently lead to better learning. Most available intervention programs are designed to improve a child's behavior in a number of domains. The MISC Program views improved functioning as an objective but as one that is secondary to the objective of affecting children's need system, creating in them such needs as these: to focus clearly on stimuli; to search for meaning; to associate, relate, compare and contrast perceptions; to seek explanations, relations, and general information beyond what is perceived through the senses. The need to please others and to summarize one's own behavior, to plan ahead, and to match one's behavior with the requirements of the task at hand.
The MISC-DS program has been ongoing at Bar Ilan University for over six years under the auspices of the Baker Center. The center provided direct services to children ranging in age from 2 months to 6 years, and to their families. Some of the children are visited at their homes by students who are instructed and supervised to raise parental awareness of the quality of mediation they provide for their children. The families participate in the program for one, two, or three years, depending on the progress of their children.
The program includes educational experiences that may be viewed on both horizontal and vertical axes. The horizontal educational dimension includes experiences of repeated exercises. The activities planned within this dimension require the application of a previously learned principle or strategy to different objects or contexts without requiring a higher level of processing. For example, if a child learned to count five objects, he is required to count five buttons, balls, boxes, or other objects. The vertical educational dimension includes a sequence of activities gradually proceeding from the easiest to the most difficult item. (Level of difficulty is determined by the level of reasoning skills required to solve a problem.) For example, a problem requiring the identification of a single numerical configuration, especially one that has already been acquired by the child, is followed by problems requiring mental manipulation of this verbal configuration; for example, eliminating one or two units from it. Starting with the numerical configuration for (:·:), subtracting and adding to it, precedes addition and subtraction of the numbers, 2, 3, and 4 (although the latter are "smaller" numbers and thus commonly considered easier to learn). In addition, this dimension includes suggestions for strategies or processes which are required to help a child progress to a higher level of thinking in order to solve a specific problem.
A special attempt was made to choose activities that are natural within the child's environment and worthwhile to him or her. For example, setting a table for dinner, peeling a banana prior to eating it, handing out candy, or slicing a cake.
Rewards were carefully designed to include verbal and actual (object) rewards distributed following correct or desired responses. Competence was mediated to the child in a manner that could be clearly understood by him or her and followed by explanations focusing the child's attention on the processes that led to the correct response. For example, most children seemed to respond well to a touch on their hand or shoulder, expressions of shared enthusiasm over the task at hand, and a combined verbal and nonverbal demonstration of what they just did "right" (i.e., "Good, you saw seven dots here, five and two make seven").
At the onset of the program, the child is presented with activities designed to teach basic concepts such as: big-small, bigger-smaller, biggest, smallest, before-after, all, none, much, little, etc. These concepts are demonstrated with sets of objects that are significantly different from each other. The program gradually proceeds to activities requiring the child to distinguish between groups that are less obviously different.
The sets of objects the child is asked to relate to at the onset of the program are homogeneous in terms of objects included in each group, but vary in number. As the child progresses through the program, he or she is required to solve problems involving heterogeneous sets of objects.
In order to progress from solving concrete exercises to solving problems on a representational level, the math problems are presented concretely (real, three-dimensional objects), followed by a pictorial presentation, followed by a visual representation of the set in dots, followed by a symbolic (numerical) presentation of the same problem.
The program includes activities that involve a transition from manipulation of objects to a pictorial configuration of numbers followed by the use of plastic numerals and finally recognition and production of graphic numerals.
The program includes the following material:
These cards describe the basic mediational principles of the program mediated to the parents. The cards relate to two main categories: (1) Presentation of the criteria of Mediated Learning Experience (how to create an adult-child interaction that constitutes a learning experience for the child). (2) Presentation of basic pedagogical principles that are essential for learning and practice in math (i.e., horizontal vs. vertical learning, proximal vs. distal teaching objectives).
Number cards include big and small configurations of the numbers From 1 to 10.
These materials include balls, plastic animals, plastic fruit and vegetables, colored cotton balls, plates, cups, cutlery, toy people, toy furniture.
Big plastic forms (circles, squares, triangles) that could be placed on the floor and stepped on and big number cubes.
Subjects were 30 children with Down Syndrome, 14 boys and 16 girls. Their ages ranged from 60 to 84 months with a mean age of 77 months (SD = 7.44) Most of the parents (both mothers and fathers) were high-school graduates. Of all parents, 66.7 percent were born in Israel, 16.7 percent were born in Europe, and 16.6 percent were born in Asia or Africa. Only two children lived in a single-parent household. Most mothers (66%) were employed and worked out of the home. Only 10 percent of the children were first born, most others were either the fourth or fifth child in their families.
The children participating in this study were divided into three groups of 10. It should be noted that no differences were found between the groups with regard to any of the above background variables.
Children participating in this group came to the University once a week for an average of six months. During these meetings the children were trained in math, using the MIM program described earlier. Parents were present during each session and were instructed how to practice the learned material with their children at home.
This group included children whose parents were invited to the University Center for general information about the MIM program once a month for six months. In this group children were not trained directly at the Center. Subjects were randomly divided into Groups 1 and 2.
This group included children who were already enrolled in various remedial programs at the University Center for periods ranging from one to three years. These children received remedial instruction in various language-related areas such as reading and music as well as math.
Math instruction was carried out in this group using the conventional method, following the commonly accepted developmental approach to math readiness. All subjects were tested at the onset of the study and following the intervention.
The following measures have been used to assess the children's level of cognitive performance: the Key Math Diagnostic Arithmetic Test (Connolly, Machtman, & Pritchett, 1986); the MacArthur Communicative Development Inventory: Words and Gestures (MacArthur, 1993) was chosen as a measure of children's active vocabulary. The Peabody Picture Vocabulary Test (PPVT) was chosen as a measure of "Passive Vocabulary," namely, understanding of words. The Visual Perception test from the Illinois Test of Psycholiguistic abilities (ITPA) was included as a measure of visual discrimination, generalization, and concept formation. The Auditory Sequential Memory test from the (ITPA) was chosen as a measure of immediate sequential memory.
A significant difference in children's performance on the Key Math Diagnostic Arithmetic Test was found in favor of experimental group 1 that had received weekly one-hour sessions of math training based on the MIM program. The Key Math mean score for the children in group 1 was 14.40 (SD = 12.07) before the intervention and 60.21 (SD = 16.89) following it. The children in this group scored as well as or better than the children in group 3 who have participated in a comprehensive intervention program including language enrichment and commonly used developmental math programs, for one to three years preceding the current study (see Figures 1 and 2). The children in group 1 have achieved significantly higher Key Math scores than those in group 2. The latter scored 13.48 (SD = 11.21) before the intervention and 27.52 (SD = 16.39) following it. A significant interaction effect for Group X Time (Before and After the Intervention) was found for the Key Math (F = 4.99, df = 1, p < .01). The children in group 1 demonstrated a better understanding of basic mathematical concepts, quantities, and the relationships between them. It should be noted that with group size as small as 10 per group and with the high level of variability in performance of DS children, differences between groups must be considerably large in order for these differences to reach statistical significance, as was the case in this study.
It may thus be concluded that an intervention based on enhancement of parental teaching behaviors in combination with a special focus on visual configurational learning of numbers had a highly significant effect on the mathematical performance of children with DS
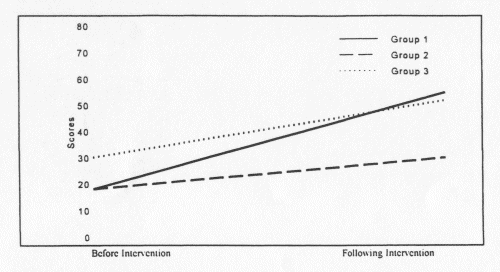 |
| Figure 1. Mean scores of groups 1, 2, and 3 on the Number Identification Subtest of the Key Math |
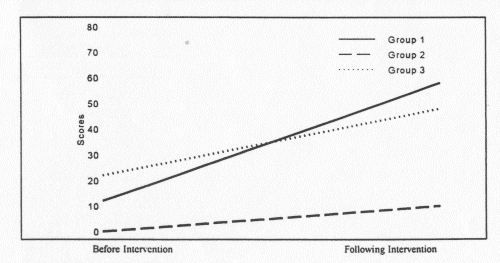 |
| Figure 2. Mean scores of groups 1, 2, and 3 on the Computation Test of the Key Math |
Children in the experimental group 1 receiving the direct MIM training for six months had a mental age score gain of 13.30 months in Receptive Language (PPVT) as compared to the other two groups who gained 6.10 and 6.60 months, respectively.
Similarly, with regard to Auditory Sequential Memory, children in the experimental group 1 gained on the average close to 9 months on the mental age score for this test as compared to a decline of 2.6 and 1.7 months for the other two groups, respectively. It should be noted, however, that the differences between the groups for both the Visual Reception and the Auditory Sequential Memory tests (on the ITPA) did not reach statistical significance probably because of the sizable variability between the subjects within each group.
Group 3, the group that had participated in a combined program of training at the Center, outscored group 1 on the MacArthur measure of communication skills, especially with regard to the number of complex sentences used in communication, and on the measure of Visual Reception. Apparently the training they have received was sufficient to raise language related skills such as concept formation (as measured by the Visual Reception measure) and sentence structure, but was not sufficient to improve their mathematical skills above the level achieved by group 1.
It should be noted that children in group 3 continued to receive Math training one hour a week (as did the children in group 1); however, the method used for teaching both groups differed. In group 3 a conventional developmental approach (including training in counting, basic concepts, i.e., more, less, same as, and simple addition and subtraction exercise) was used as compared with the MIM approach used in training of group 1.
At the onset of the study all the participants had very little awareness of quantity, or of any mathematical concepts. None of the children could count correctly or recognize any of the numerals. None of the children understood basic concepts such as more, less, first, second, third, and last. Following the intervention, 8 of the 10 children in experimental group 1 (3 out of 10 in group 2; 5 out of 10 in group 3) learned to understand quantities of up to 10 objects. They understood concepts such as more, less, same as, smallest, largest, etc. In addition, these same children learned to count correctly up to 10. All group 1 children could count correctly up to the numbers for which they had learned the visual configuration presented in the MIM program. One child could count up to 6, but consistently skipped number 6. She overcame this difficulty as soon as she had learned to recognize the configuration for 6 and the numeral 6. The fact that young children can count does not mean that they understand the meaning of numbers. For example, even when young children count correctly 10 balls in a basket, they may not necessarily be able to answer correctly the question, How many balls are there in the basket?
The children who participated in the intervention learned how to count correctly and were aware of the fact that the last number counted represents the number of objects in the group. For all children it took many trials to learn the first configuration, namely 5 (:·:). Once they had mastered it, they still found it difficult to learn the configuration for 4, but following 5 and 4, configurations of other numbers were acquired much more quickly.
Once the children learned the 5,4,3,2,1, configurations going up beyond 5 were much easier to learn since most children were using configurations they had already acquired (i.e., 5 + 1, 5 + 2, etc.).
It is interesting to note that two mothers in the experimental group attempted to help their children learn math by teaching them how to count in the commonly known manner. Those two children found it most difficult to grasp the visual configurations and were considerably slower in solving math problems than the other children in the group.
One of the children in group 1, who is enrolled in a regular school program, was doing quite well in reading and writing but had considerable difficulties in math. Following the program, her teacher reported that she had made considerable progress in math and revealed a good understanding of numbers. Teachers and parents reported that children who had enrolled in the MIM program expressed enthusiasm and excitement when they recognized numerals written on road signs, products, announcements, or any other object in their environment. Identifying most numbers and reading them aloud became a favorite learning game for them. Such behaviors were not reported for the children in groups 2 and 3.
The most important research questions remaining to be explored following this study are related to the sustainability of the gains in mathematical thinking found in this study following the use of the MIM program and the question of how far children with DS can advance in mathematical thinking through the use of the MIM approach.
Since many of the difficulties that children with DS have in understanding and using numbers are associated with a slower, rather than a different developmental pattern from that of nonretarded children, it may be assumed that young nonretarded children with learning disabilities in mathematics have some or all of the same difficulties. Thus, if other methods fail to enhance their understanding and use of numbers in everyday life, it may be helpful to consider the MIM approach, shifting the initial processing of the number concepts from the sequential, verbal left hemisphere to the figural, simultaneous (nonsequential) right hemisphere mode of processing. This approach should be considered within the more comprehensive attempt to enhance the quality of parent-child mediation within the child's natural environment, culture, and family.
Bereiter, C., & Engelmann, S. (1966). Teaching disadvantaged children in the preschool. Engelwood Heights, NJ: Prentice-Hall.
Buckley, S. (1985). Attaining basic educational skills: Reading, writing and number. In D. Lane & B. Stratford (Eds.), Current approaches to Down's syndrome (pp. 315-342). London: Holt, Rinehart & Winston.
Cicchetti, D., & Beeghly, M. (1990). An organizational approach to the study of Down syndrome: Contributions to an integrative theory of development. In D. Cicchetti & M. Beeghly (Eds.), Children with Down syndrome: A developmental perspective (pp. 29-62). Cambridge, U.K.: Cambridge University Press.
Cicchetti, D. & Mans-Wagener, L. (1987). Stages, sequences, and structures in the organization of cognitive development in Down syndrome infants. In L. Uzgiris & J. McV. Hunt (Eds.), Research with scales of psychological development in infancy (pp. 95-107). Urbana: University of Illinois Press.
Cicchetti, D., & Sroufe, L. A. (1976). The relationship between affective and cognitive development in Down syndrome infants. Child Development, 47, 920-929.
Connolly, A. J., Machtman, W., & Pritchett, E. M. (1986). Key Math Diagnostic Arithmetic Test. Circle Pines, MI: American Guidance Services.
Feuerstein, R. (1979). The dynamic assessment of retarded performers. Baltimore, MD: University Park Press.
Feuerstein, R., Rand, Y, & Rynders, J. E. (1988). Don't accept me as I am-Helping "retarded" people to excel. New York: Plenum Press.
Fishier, K. (1975). Mental development in Mosaic Down syndrome as compared with Trisomy 21. In R. Koch & F. de la Cruz (Eds.), Down's syndrome (mongolism): Research, prevention and management (pp. 87-98). New York: Brunner/Mazel.
Fowler, A. E. (1990). Language abilities in children with Down syndrome: Evidence for a specific syntactic delay. In D. Cicchetti & M. Beeghly (Eds.), Children with Dawn syndrome: A developmental perspective (pp. 302-328). Cambridge, U.K.: Cambridge University Press.
Gibson, D. (1978). Down's syndrome: The psychology of mongolism. Cambridge, U.K.: Cambridge University Press.
Hill, P. M., & McClure-Nicholich, L. (1981). Pretend play and patterns of cognition in Down syndrome children. Child Development, 52, 1168-1175.
Hodapp, R. M., & Zigler, E. (1990). Applying the developmental perspective to individuals with Down syndrome. In D. Cicchetti & M. Beeghly (Eds.), Children with Down syndrome: A developmental perspective (pp. 1-28). Cambridge, U.K.: Cambridge University Press.
Hook, E. (1982). The epidemiology of Down syndrome. In S. Pueschel & J. Rynders (Eds.), Down syndrome: Advances in biomedicine and the behavioral sciences. Cambridge, MA: Ware Press.
Horowitz, C. H. (1987). Math without tears. Journal of Reading, Writing and Learning Disabilities International, 3( 1), 31-40.
Irwin, K. C. (1989). The school achievement of children with Down's syndrome. New Zealand Medical Journal, 102, 11-13.
Kelly, M. M., & Schoen, S. F. (1988). It worked in my classroom: A social and academic behavior change program. Research report. La Salle University. Typescript.
Klein, P. S. (1990). The more intelligent and sensitive child (MISC) program for D.S. children. In E. Chigier (Ed.), Looking up at Down syndrome (pp. 181-191). London, U.K: Freund.
Klein, P. S. (1992a). Assessing cognitive modifiability of infants and toddlers: Observations based on mediated learning experience. In H. C. Haywood & D. Tzuriel (Eds.), Interactive assessment (pp. 233-250). New York: Springer.
Klein, P. S. (1992b). More intelligent and sensitive child (MISC): A new look at an old question. International Journal of Cognitive Education and Mediated Learning, 2(2), 105-116.
Klein, P. S. (1996). Early intervention: Cross cultural application of a mediatorial approach. New York: Garland Pub.
Klein, P. S. (1997). A mediational approach to early intervention. This Journal, 1, 61-85.
Klein, P. S., & Alony, S. (1993). Immediate and sustained effects of maternal mediating behaviors on young children. Journal of Early Intervention, 17(2), 1-17.
Klein, P. S., & Feuerstein, R. (1984), Environmental variables and cognitive development: Identification of potent factors in adult-child interaction. In S. Harel & W. N. Anastasio (Eds.), The at-risk infant: Psycho-socio-medical aspects (pp. 369-377). Baltimore: Paul H. Brooks.
Klein, P. S., Raziel, P., Brish, M., & Birenbaum, E. (1987). Cognitive performance of 3 year old born at very low birth weight. Journal of Psychosomatic Obstetrics and Gynecology, 7, 117-129.
Klein, P. S., & Wieder, S., & Greenspan, S. I. (1987). A theoretical overview and empirical study of mediated learning experience: Prediction of preschool performance from mother-infant interaction patterns. Infant Mental Health Journal, 5(2), 110-129.
Kopp, C. (1983). Risk factors in development. In P. Mussen (Ed.), Handbook of child psychology, Vol. 2. New York: Wiley.
Lister, C., Leach, C., &: Riley, E. (1989). The development of understanding of quantity in children with Down's syndrome. Early Child Development and Care, 49, 57-66.
MacArthur, D. (1993). The MacArthur communicative development inventory: Words and gestures. San Diego, CA: Singular Publishing Group.
Mosley, F. (1986). Count me in. Games for all. Mathematics in School, 15(1), 6-9.
Murphy, J., Bates, P., & Anderson, J. (1984). The effect of self-instruction training on counting skills of pre-school handicapped students. Education and Treatment of Children, 7(3), 247-257.
Sharma, M. C., & Loveless, E. J. (Eds.) (1986). The work of Dr. Ladislav Kosc on dyscalculia. Focus on Learning Problems in Mathematics, 5(3-4), 47-119.
Stern, M. (1987). Using the Stern blocks. Journal of Reading, Writing and Learning Disabilities International, 3(1), 21-30.
Weisz, J., & Zigler, E. (1979). Cognitive development in retarded and nonretarded persons: Piagetian tests of the similar sequence hypothesis. Psychological Bulletin, 86, 831-851.
Yarmish, R. (1988). Numerical equivalence and the developmentally impaired. Focus on Learning Problems in Mathematics, 10(4), 31-50.
This study was supported by a grant from the Annenberg Foundation 1994-1995, and by the I. B. Harris Foundation, 1997.
Dr. Klein is Head of Early Childhood Programs and Director, Baker Center, Bar-Ilan University, Israel.
Mary Arieli is an Early Childhood Education Specialist, Baker Center, Bar-Ilan University, Israel.